7Limits of Computation

In this section, we discuss the limits of computation and show that there are some uncomputable problems.

Before we go further, let us clarify what we mean by computable. The Church-Turing Thesis is equivalent to the statement that every computable problem can be solved by a Turing machine. Moreover, we expect that a computational process should always complete in finite time and not run forever. Thus, we will use decidable to mean computable and consequently, undecidable problems are uncomputable.

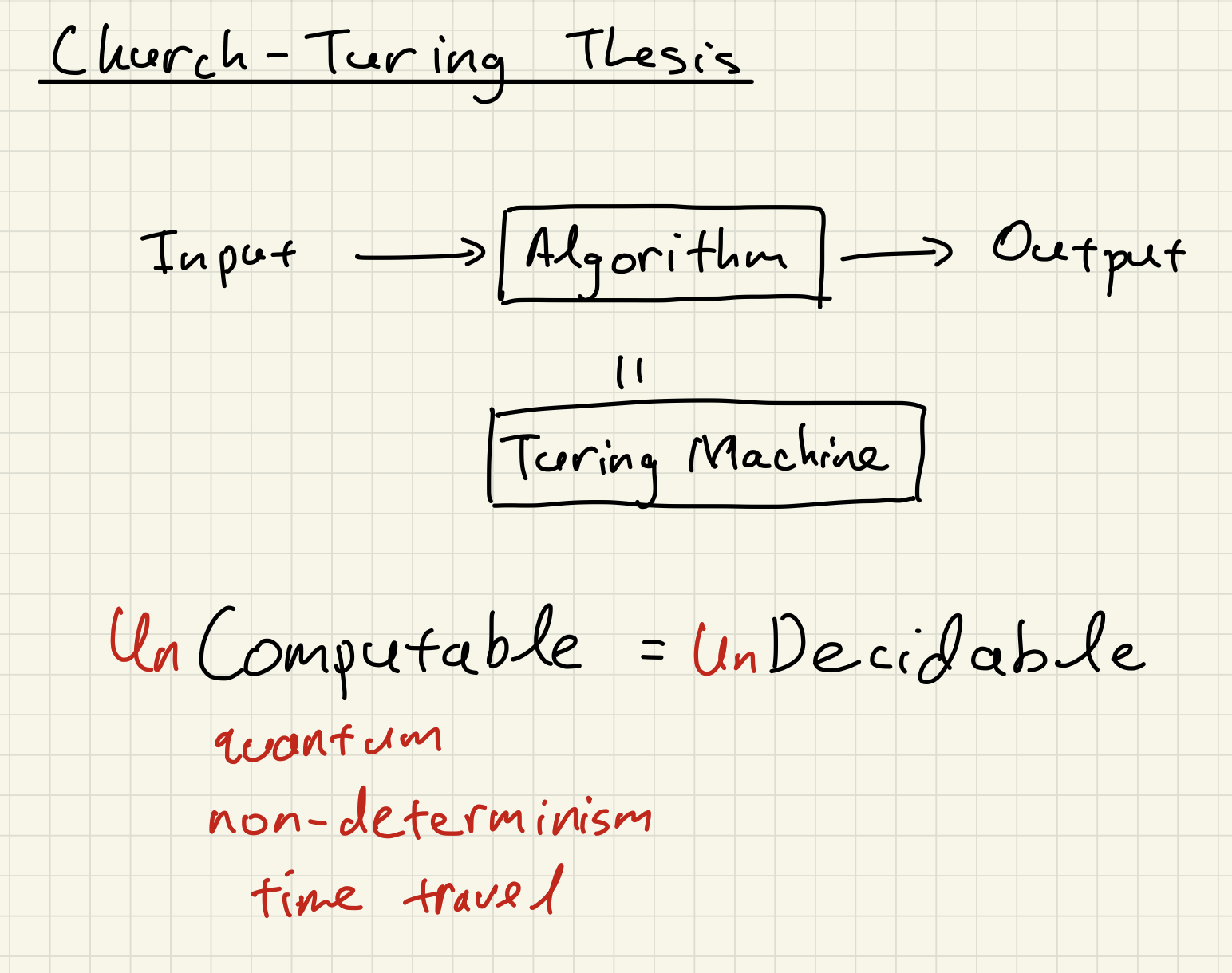
Note that decidable only means that the computation will eventually terminate. This allows for computation that takes exponential time and space, for example. For actual applications, we also want computation to be efficient.

Thus, the Church-Turing Thesis implies that undecidable problems cannot be solved even if we allow the computation to run for an impractical amount of time and space. Even worse, it means that there is no future physical hardware or algorithmic technique that can be invented that will solve these problems.

At a practical level, understanding the limits of computation is important as there are natural problems that have practical applications that are undecidable. These include a vast array of problems in program analysis such as deciding if a given program can ever run into an infinite loop, and deciding if two programs have equivalent behavior.

Being able to identify whether a problem is undecidable is useful as it saves us time designing an algorithm for the problem.