Skip to article frontmatterSkip to article content

5.5Summary

The University of Melbourne

In this section, we covered context-free languages and saw two equivalent definitions:

  1. (Machine model) Context-free languages are those that are recognized by non-deterministic pushdown automata.

  2. (Generative model) Context-free languages are those that are generated by context-free grammars.

Intuitively, a pushdown automata is a finite automata augmented with a stack, and context-free grammars have the additional power of recursion over regular expressions.

5.5.1Languages that are not context-free

A canonical language that is not context-free is {0n1n2n∣n≥0}\{0^n1^n2^n \mid n \geq 0\}.

While pushdown automata can some form of unbounded counting, they are still very limited. Intuitively, the PDA that recognizes the language {0n1n∣n≥0}\{0^n1^n \mid n \geq 0\} does so by matching the $1$s that in the second half with the $0$s that appear using the stack.

5.5.2Story so far

We summarize our current knowledge of the landscape of languages in the following diagram.

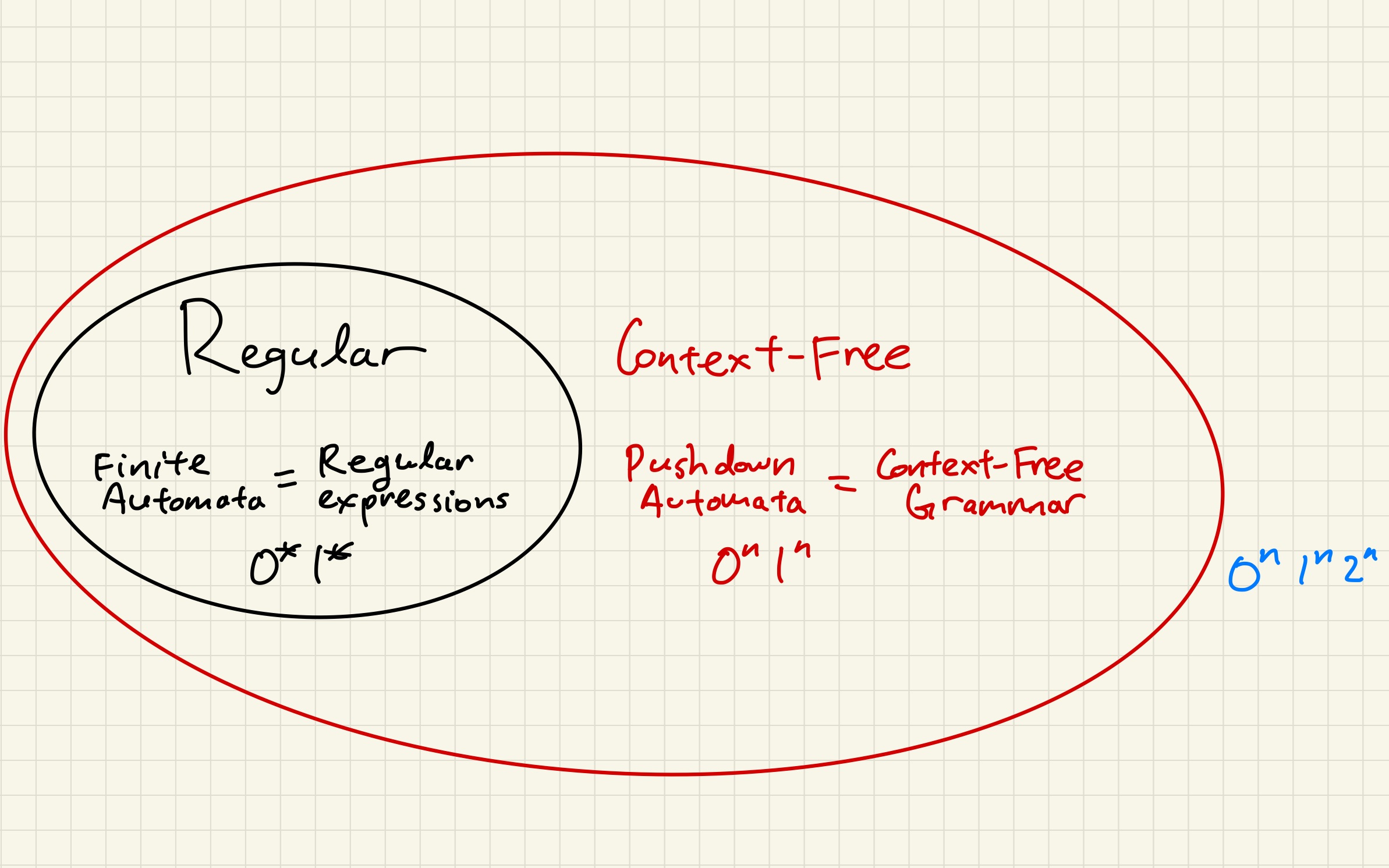
Current knowledge of landscape of languages. The set of context-free languages are those that are recognized by nondeterministic pushdown automata and generated by context-free grammars. The two models are equivalent. An example non-regular language is 0^n1^n. An example language that is not context-free is 0^n1^n2^n.

Current knowledge of landscape of languages. The set of context-free languages are those that are recognized by nondeterministic pushdown automata and generated by context-free grammars. The two models are equivalent. An example non-regular language is 0n1n0^n1^n. An example language that is not context-free is 0n1n2n0^n1^n2^n.

Models of Computation
CFG = PDA
Models of Computation
Computable Languages