5.2Pushdown Automata
Intuitively, a pushdown automata is a finite automata but with a stack. The stack is unbounded which gives the pushdown automata unbounded memory. However, the pushdown automata has limited access to the stack: it can only read and remove the top element of the stack (a pop operation) and write a new element at the top of the stack (a push operation).
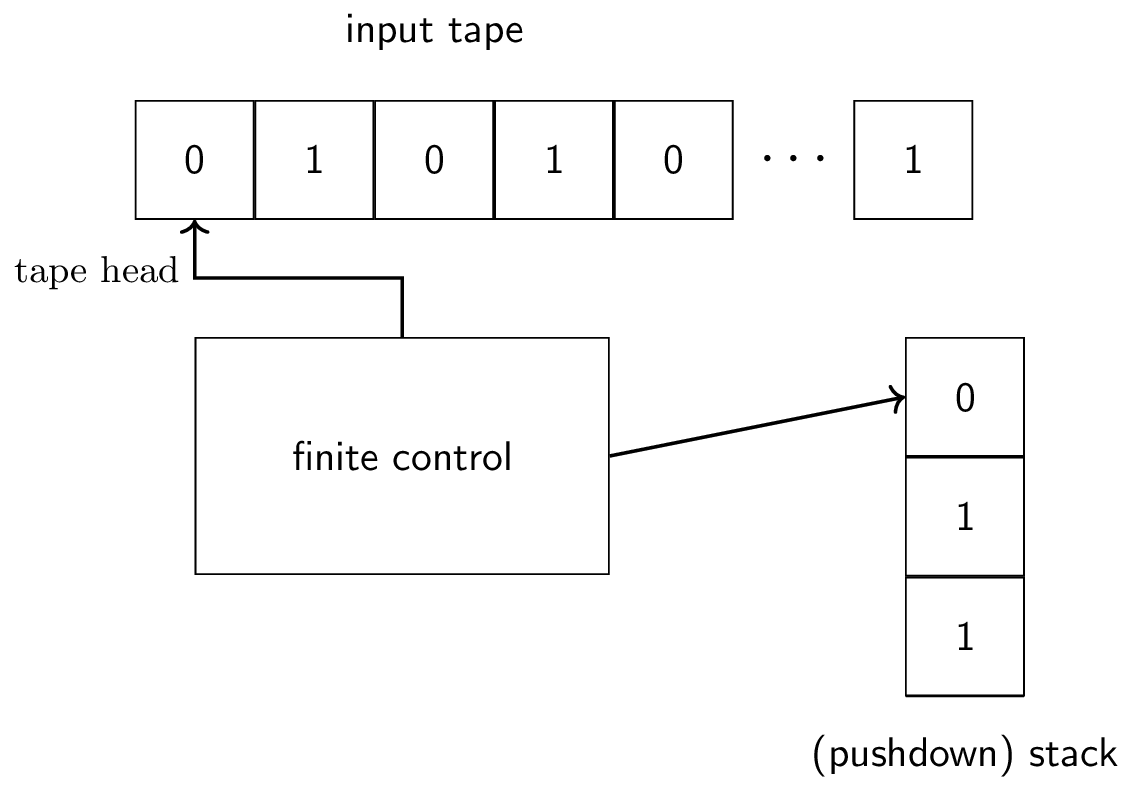
Schematic diagram of a pushdown automata.
Nevertheless, it can do simple counting which lets it recognize the language .
5.2.1Pushdown automata for ¶
Let us first see what a deterministic pushdown automata (DPDA) consists of and what it can do. It consists of a set of states (with one initial state and some are marked as accepting) and its transition function defines rules for state transitions with the following template:
If we are currently in state , the next input symbol is and the top symbol of the stack is , then go to state and either leave the stack alone, or apply a push or pop operation to the stack.
We also allow the DPDA to make -transitions without consuming the next input symbol.
The DPDA processes an input string as follows:
Start at the initial state
For each input symbol (starting from ), follow the applicable transition
After all input symbols have been processed, accept the string if the final state is an accepting state and reject otherwise.
Unlike finite automata, it turns out that nondeterministic pushdown automata are strictly more powerful and can recognize languages not recognizable by deterministic pushdown automata. So, in the rest of this section, we will stick with nondeterministic pushdown automata.